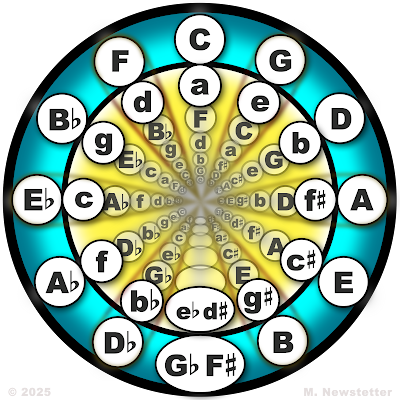
A journey into the eye of the hurricane of tonality. What is meant by "tonal center" and how does that concept play out on the guitar?

 Explorations of the Double Harmonic scale.

—Also known as the Byzantine scale, Arabic scale, and by other names in different musical traditions.—

The major mode of this scale is symmetrically structured, comprising two identical internally symmetrical tetrachords (4-note scale fragments) with three semitones (halfsteps), two augmented seconds and one whole-tone (wholestep).

The minor mode is rooted in the 4th degree of the major. It is also called a Gypsy Scale, or Hungarian Scale, among other names.

Applying this scale on the guitar means approaching it within its own frame of reference rather than seeking to modify existing Diatonic scale patterns.

In the diagrams here, the scale has the tonic "C". If we were to compare it to the C major scale, we'd say it has a flatted 2nd and 6th. But using that fact as a method for navigating the scale on the fretboard means we'd always be thinking about those major 2nd and 6th notes that we're altering, rather than recognizing the unique forms of the scale on their own.

Since the scale has its own unique symmetries, why not just start from there. Forget about altering anything ... forget about Ionian mode. This scale is not an alteration of Ionian mode, it has its own history and its own logic. To really get it you need to forget everything you know about major scales ...

Think what it would be like if this was the first scale you learned.

The Circle

 Circle of 5ths / 4ths showing all the notes of each key as radial spokes:

Notes of each spoke are arranged in descending 3rds starting from the major tonic inward toward the center.

The circle organizes all the diatonic keys based on perfect 5th (clockwise) and perfect 4th (counter-clockwise) intervals. The tonics of the major keys (Ionian Mode) form the outer ring, accompanied by the relative minor tonics (Aeolian Mode) placed one level in toward the center.

We can extend the logic further by adding all the notes of each key in descending 3rds, just as the minor tonic is a 3rd below the major. So, starting from C at the top of the circle, we read the notes C, A, F , D, B, G, E ... essentially a descending arpeggio.

The upper and lower case letters in the diagram represent the major and minor qualities of each 3rd interval for which that note is the (root) ...  and can also be treated as the finals of their respective modes: Ionian, Lydian and Mixolydian have major 3rds, so they are upper case. Dorian, Phrygian, Aeolian and Locrian have minor 3rds, so they are lower case.

From the outside in, the modes are: Ionian, Aeolian, Lydian, Dorian, Locrian, Mixolydian and Phrygian. 

Numerically, they are I, vi, IV, ii, viiº, V, and iii.

The "Circle of Fifths" is something to ponder. A schematic for the diatonic system which reveals many interval relationships in a way that comports well with the nature of music. 

Paradoxically, if we approach musical concepts as circular, as a continuum with not fixed beginning or end, many things become clearer. Starting points and ending points in music are essentially contextual.

The Speed of Pitch

What we call "octaves' are the phenomenon of a 2:1 frequency ratio. Our perception of octaves as "the same note" seems to be a deeply embedded sense. No one questions the practice of giving two different notes the same name when they are one octave, two octaves, three octaves or more apart from each other.

Why is this?

What is it about this 2:1 ratio that we sense as "the same"?

Consider the effect of clapping at a steady speed, then doubling the speed of clapping. Or have another person clap along with you but at double the speed and stay in sync.

You'll notice that the claps will perfectly align every other beat, so that the lower speed clap is effectively embedded in the faster one. The ratio of the frequency of your clapping is the same as an octave. This provides a clue as to the reason octaves are perceived as the same.

In the ear, sound is processed by setting in motion some 15,000 tiny specialized hair cells, each of which has between 50 and 300 filaments projecting from it, called stereocilia. These hairs are contained in a fluid filled spiral shaped structure called the cochlea. The hairs and the stereocilia in each ear resonate with specific frequencies and transmit that information to the auditory cortex of the brain which has specialized neurons for each frequency and range of frequencies. So your brain is always sensing the frequencies of every sound and is able to recognize the ratios between those freq
uencies.

Exactly how the brain can calculate the precise frequency ratios between all the pitches we hear is quite complex and still somewhat mysterious, but it is probably connected to the brain's ability to sense time as sequential events based on it's own brainwave frequencies and the embedding of resonations in its neural network. Regardless of the precise mechanism, it's clear that we are very good at perceiving the ratios between notes regardless of their absolute pitch.

In other words; if you hear a melody in one key, and then the same melody in another key, you recognize it as "the same" because you recognize the ratios between the frequencies of every note in the melody, rather than relying only on the absolute pitches of the individual notes. The melody of the song Happy Birthday in the key of C would be:

and In the key of F:

Now, clearly the notes are not the same in both keys, but that doesn't prevent us from hearing both of them as the same song, even if one is higher in pitch and one is lower overall.

Our awareness of pitch as proportional relates to our sense of time and, therefore, to our sense of motion ... which is in turn connected to our experience with gravity and other physical forces. All this is at the heart of why we naturally regard higher (faster in time) frequencies as physically "up" and lower (slower in time) frequencies as physically "down". 

Because differences in note frequencies are not really tangible on a conscious level (we can't discern the individual oscillations of hundredths of a second) music affects us subconsciously, subliminally. We feel it without knowing exactly why.

We can consciously identify a 4/4 beat ... we can clap and we can count the beats. So our relationship to rhythm is not so mysterious. We can be satisfied that dancing to a beat is a relatively simple matter. The mysterious nature of our perception of melody and harmony is does not mean that melody and harmony are any less real than the beating of a drum or tapping your foot. Sustained tones are just faster oscillations. The same essential physical phenomenon as individual drum beats. 

The video below explores this subject from a practical and philosophical perspective:

Modal Arpeggios — Arpeggiometry

 

Each of these arpeggio patterns encompasses all six strings and include all the notes of any diatonic key spanning two octaves. 

They are ordered in 5ths:

II, VI, III, VII, IV, I, V.

Try playing each of them rooted on the same fret position and notice the difference in fingering as you go from one to the next.

Diagrams PDF

Watch the Arpeggiometry Video for more about this post.

More Modal Madness Galore!

Before you venture into this ... please study the previous post: 

https://fretography.blogspot.com/2023/03/diatonic-symmetry-galore.html

Now ... where were we?

Ok ... we're making connections between modes and keys across the diatonic system. Modes do not only exist in separate keys with walls around them. The cross key relationships we find in so much music have their own logic, grammar and flow.

The character of each mode becomes a pathway from one musical idea to another. We sense when the key has changed, and it is modality that provides the framework of coherence of the harmonic and melodic threads. 

Since Dorian mode is diatonically central, lets see how it connects to the seven keys drawn from its traverse of natural tone finals ...

The natural tones across the top, bottom, left and right of each diagram are the finals of seven modes in  seven keys. The tonic of each key is found where the blue lines cross.

The blue lines are anchored on each mode with D as the final.

Since all the modes stem from natural tones, it's easy to trace the connections between the keys through their modes. Each mode receiving this treatment will yield a different patter.

Particularly relevant is the connection between the placement of the secondary keys (blue lines) and the common tones (grey lines) and the symmetrical modal relationships.

Look at the palindromic pairs of modes ... those modes who's interval structures mirror one another: 

 

It becomes clear that while there are symmetries to be found in the treatment of the natural tonic (shown in the previous post), the symmetry is far clearer when applying the logic to the natural supertonic ... D.

Notice that all seven converged keys have natural tonics, where using C as the finals of all the modes led to the keys of C, G, F, Db, Eb, Ab and Bb. Also notice the the blue line crossings always converge with a grey line, which does not happen with the yellow lines in the previous post.

The symmetry is clear, which is to be expected with Dorian mode, and why this mode is so essential as a starting place for understanding the Diatonic System

Modal Symmetry Galore

The symmetry built into the Diatonic system has many manifestations. One of the most compelling is the phenomenon of modal common tones.

Deep Symmetry

The modes form palindromic interval groupings ...

Ionian and Phrygian, 

Locrian and Lydian, 

Aeolian and Mixolydian,

... and Dorian mode ...

The intervals within each mode are part of the overarching Diatonic symmetry. Study the interval structure of the modes ... notice the palindromic pairings:

Common Tones connect seven keys in a modal continuum ...

Modal Common Tones

When the notes of Major scale (Ionian mode) each become the tonic of a new key there is but one note common to them all. In the Key of C are the notes C D E F G A B ... the scale will include the complete octave — C D E F G A B C.

Make each of these natural tones the Tonic, and you have seven keys, and within each of them is the note 'E' ... the III of the original key. There will be no other note to find a place in all seven keys.

That's interesting enough, but there's more!

Do this with all of the seven Modes, and you'll find the correlation between Mode's interval symmetry and the Common Tone Counterpart groupings.

Common Tone Counterparts are those notes that link the diatonic symmetry due to their corresponding key degrees.

Just as Ionian and Phrygian are a palindromic pair, the notes C and E are positioned symmetrically around the central note of the key: D ... as are B and F, as well as A and G ... and their respective modes.

These images show the common tones in each mode. In each case — within seven keys which have Natural tones as their tonics:

(The tonics are always found in the column with C at the top and bottom, i.e.: the tonics for the Phrygian mode above are C Db Eb F G Ab Bb. The tonics for Aeolian mode below are C D Eb F G Ab Bb.)

The reciprocal relationships between modes and their counterpart common tones is profound!

... It reinforces the centrality of the Tritone ...

... and of the Dorian mode which stems from the 2nd Key Degree ...

All of this plays out on the fretboard with absolute consistency.

Notice the rotational symmetry of Key Degree relationships on the fretboard within the upper and lower string groups:

I is opposite III

VII is opposite IV

VI is opposite V

and II is opposite II

Just how the fact of this symmetry can factor into music in practice is a complex subject. Save to say that awareness of a thing naturally generally precedes one's understanding of it. 

The Modal Common Tone can be a pivot between keys. It has a different function in each, but ... there it is. Is there a difference between key transitions with or without common tones?

There must be a mathematical formula which expresses all this. Since I'm about as good a mathematician as I am a brain surgeon, I'll leave the math to others.

Also of interest is how these commonalities align with the Circle of 5ths and 4ths. 

On the left side of the circle are flat keys (keys containing one or more flat) and on the right side are sharp keys (keys with one or more sharp). The interval symmetry of counterpart modes plays out in the incidence of flat and sharp keys expressed by each mode. Since the key of C is all natural tones, the remaining keys are an equal number, with  F# and Gb each occurring only once — through Lydian and Locrian respectively — among the common keys ...

Common Keys

C Ionian: C, D, E, F, G, A, B

E Phrygian: C, Db, Eb, F, G, Ab, Bb

________________________________

F Lydian: C, D, E, F#, G, A, B

B Locrian: C, Db, Eb, F, Gb, Ab, Bb 

________________________________

A Aeolian: C, D, Eb, F, G, Ab, Bb

G Mixolydian: C, D, E, F, G, A , Bb

________________________________

D Dorian: C, D, Eb, F, G, A, Bb 

Among keys which are not found within each mode is the following array ...

Non-common Keys:

 

C Ionian: Bb, Eb, Ab, Db, and Gb or F#

E Phrygian: B, E, A, D, and Gb or F#

________________________________

F Lydian: Bb, Eb, Ab, Db, F

B Locrian: B, E, A, D, G

________________________________

A Aeolian: B, E, A, Db, and Gb or F#

G Mixolydian: B, Eb, Ab, Db, and Gb or F#

________________________________

D Dorian: B, E, Ab, Db, and Gb or F#

A careful analysis of the balance of sharp keys and flat keys within counterpart modes will reveal a clear symmetry vis-a-vis the Circle of 5ths as they are equally distributed.

------------------------------------------------

What do we do with this knowledge? 

That question can best be answered by asking another question:

"What do we do with nouns and verbs?" 

On the most basic level, these ideas are simple matters of fact ... like the Circle of 5ths. The interlocking relationships between common modes across multiple keys builds upon the Major key-Minor key paradigm usually associated with the Circle of 5ths. What applies to Ionian and Aeolian modes also factors into connections between all the other modes, and that's not limited to I - IV - V patterns.

The common tone connection brings chromaticism into the mix. How does that relate to, say, Melodic and Harmonic Minor ?

Recapping: Modal Logic

Any mode, when used as the source of seven tonics (or finals), will share with all of them one — and only one — common tone. That common tone will be the final of its palindromic counterpart mode.

For example:

The common tone of Ionian mode is its 3rd degree. That note is the final of Phrygian mode, which has a common tone on its 6th degree ... which is the final of Ionian mode.

The final of Lydian mode is its 4th, and the final of Locrian mode is its 5th. 

The final of Aeolian mode is its 7th degree, and the final of Mixolydian mode is its 2nd ...

Since Dorian mode is its own palindrome, its common tone is its own final ... note number 1.

------------------------------------------------

Secondary Source Keys*

The Secondary Source Key (or 'Parallel Source Key') for each modal group is the major key built from the modal scale with the note C as its final. There is an inverse relationship between the place of the tonic of each Secondary Source Key and the degree of the mode itself in the major scale overall. (*This terminology is original. I'm unaware of any existing term for this precise phenomenon.)

The Secondary Source Key for each mode:

C Ionian (tonic mode) =  C ... its own tonic.

C Phrygian (mediant mode) = Ab ... it's own submediant.

 C Locrian (leading tone mode) = Db ... its own supertonic

C Lydian (subdominant mode) = G ... its own dominant

 C Aeolian (submediant mode) = Eb ... its own mediant

 C Mixolydian (dominant mode) = F ... its own subdominant

and for C Dorian (supertonic mode) = Bb its own subtonic.

Here are the diagrams with the major tonics indicated by yellow highlights. Notice that the major tonic of the secondary source key, in each case, is where the two lines converge:

 

These layers of diatonic symmetry — each layer being balanced within itself — form overlapping asymmetries which in turn reveal interesting commonalities. Though the modal common tones follow the intervalic mirroring of mode pairs, the secondary source key relates the degree of the mode final within the original source key, to its own internal degrees. 

Put another way; the diatonic place of each mode's final has an inverse interval relationship to its relative major tonic. II is the inverse of bVII, III is the inverse of VI, IV is the inverse of V ... I is, of course, is own inversion.

The particular aspects of modal commonalities across keys delineated here are by no means the only possibilities, but they represent a way into this realm harmonic complexity.

...

Next: https://fretography.blogspot.com/2023/03/more-modal-madness-galore.html